
- 1. 스테핑모타란 무엇인가
스테핑모타는 외부의 DC전압 또는 전류를 모타의 각 상단자에 스위칭방식으로 입력시켜 줌에 따라 일정한 각도의 회전을 하는 모타이다. 따라서 이는 일종의 디지털 제어방식의 기기로서 일반적인 아나로그 전원보다는 디지털 펄스형식의 제어에 적합하다.
즉, 디지털펄스 1개에 1개스텝 ( 본 제품은 기본각도가 1.8˚임 )에 해당하는 회전각만큼 정확한 회전운동을 하게 되며, 입력펄스의 수와 단위시간당 펄스입력속도에 정확히 비례하여 연속운동을 하게 된다 (단, 이때의 연속운동이란 불연속운동이 펄스입력속도가 증가함에 따라 마치 연속운동의 효과를 내는 것처럼 보일뿐이다. ).
- 2. 스테핑모타의 회전운동 :
스테핑모타는 크게 적층강판에 코일을 권선한 스테이터(고정자), 그리고 영구자석과 적층 강판의 조합으로 만들어진 로터(회전자)로 이루어져 있다. 이의 회전운동은 DC모타의 원리를 참조하기 바랍니다.- 3. 스테핑모터 관련용어
3.1 토르크 ( Torque ) :
로터의 회전축 중심으로부터 1Cm 또는 1m 떨어진 부하(물체)를 단위시 (1초)에 1Cm 또는 1m를 움직일 수 있는 힘 ( 단위 : gfcm 또는 Kgfcm 등)
최대정지토르크 ( Holding Torque or Stall Torque or Static Torque) :
정격전원의 에너지를 모타에 인가시켰을 때 모터의 축을 외부의 힘으로 움직이게 하는 데 필요한 토르크
부하토르크 ( Pull-out Torque ) :
일정한 펄스속도로 구동되고 있는 모타축이 정지하지 않고 또한 입력펄스속도에 정확히 동기하여 대응할 수 있는 최대부하의 크기.
부하의 크기가 이 이상일 때는 이 속도에서 모타축이 정지하거나 입력펄스 속도를 따르지 못한다.- 자기동토르크(Pull-in Torque ) :
일정한 펄스속도를 가감속 없이 모터에 인가하였을 때 입력펄스에 동기 대응하여 회전운동할 수 있는 최대 부하의 크기
이 보다 큰 부하의 경우는 입력펄스속도를 가속/감속시켜야 된다.
3.2 오차
스텝각도오차( Step Angle Accuracy ) :
스테핑모타의 회전각도의 정확도를 표시한다.
이는 한스텝 한스텝 모타를 회전시켰을 때 회전거리의 정확도를 나타내며 이는 히스테리시스오차(hysteresis error)를 포함시키지 않는다.
정지각도오차( Positional Accuracy ) :
2상여자( Full-step Driving )로 모타를 360˚회전시켰을 때 최대각도오차. 이는 360˚회전시 각스텝마다의 오차중 (+)최대치와 (-)최대치의 1/2값을 말한다.
히스테리시스오차(hysteresis error) :
모타를 정방향으로 회전시켰을 때 정지한 위치와 역방향으로 회전시켰을 때 정지한 위치는 약간 다르며 이 때의 위치차이를 말한다.
3.3 모타의 속도
구동주파수(Pulse-rate or Step-rate or Speed) :
스테핑모타를 연속구동시키는 전원펄스 신호를 단위시간(초)당의 입력펄스수로 표시한 것. ( PPS : pulses per second의 약자 )
자기동영역(Start-Stop region) :
입력신호에 대해 한정된 부하범위내에서 가감속 없이 즉시 기동,회전,정지를 할수 있는 토르크-구동주파수 영역
최대자기동주파수(Max Start-Stop region or Instantaneous Start-Stop region ) :
무부하상태에서 가감속 없이 즉시 기동,회전,정지를 할 수 있는 최대 구동주파수
구동영역(Slew-region) :
자기동영역을 초과한 부하-토르크영역으로서 구동주파수를 가/감속의 방법으로 확대구동시킬 수 있는 영역
최대응답주파수(Max Slewing Pulses rate ) :
Slew-region의 최대구동주파수
잔여진동시간(Settling-time) :
스테핑모타는 회전상태의 회전자가 어느지점에 왔을 때 정지신호를 받은 순간부터 그 지점에서 즉시 정지하지 못하고 대략 3-5%정도의 각도 오차범위내에서 전후로 진동을 하다 정위치에 정지하게된다. 이 신호를 받은 순간부터 진동이 완전히 없어져 정위치에 서 있을 때까지의 시간을 말한다.
응답시간(Response time) :
스테핑모타에 펄스신호를 인가시켰을 때, 신호가 주어진 시간으로부터 첫 기본스텝각도에 도달하기까지의 시간
3.4 모타의 특성
잔여진동(Damping ) :
회전상태의 회전자가 정지신호를 받게되면 그 정지점에 즉시 정지하지를 못하고 일정시간 동안 전후진동(잔여진동)을 하다가 정위치에 오게된다.
공진(Resonance) :
모타자체의 기계적특성과 전기적특성이 어느 구동주파수영역에 이르게 되면 급격히 진동을 일으키거나 출력토르크를 저하시키게 된다. 이를 공진이라 하며, 저속(저주파)대역에서는 대개 150-250pps에서 발생한다. 이 공진은 마찰부하나 관성부하 또는 모타의 권선조건 등에 따라 변하게 되며, 운전방식과 구동회로에 따라 어느정도 변화된다.
3.5 운전방식(구동방식 : Driving Mode or Method )
유니폴라/유니폴라드라이브(Unipolar / Unipolar-Drive) :
외부의 입력전원을 모타 상에서 한 방향으로만 흐르게끔 결선한 것. 또는 각 모타 상의 권선에 인가한 입력전원이 항상 같은 극성을 갖게끔 구동시키는 모타, 구동방식.
이 유니폴라모타와 유니폴라드라이버는 6선이나 8선을 필요로 한다.
바이폴라/바이폴라드라이브(Bipolar / Bipolar-Drive) :
모타의 동일권선에 입력펄스의 극성을 바꿔주는 방식. 출력단은 약간 복잡하지만, 유니폴라 구동방식에 비해 각도의 정밀도가 좋으며 저속에서 보다 높은 토르크를 얻을 수 있다.
이 바이폴라모타는 4,6,8선의 모타를 사용할 수 있으며 대개 6선보다는 4,8선의 모타를 사용시 효율이 더 좋다. 이 바이폴라드라이브에는 직렬연결, 병렬연결 방식과 단전원구동 및 2전원 구동방식이 있다.
쵸핑드라이브(Chopping-drive) :
전류검출저항에서 전류에 합당한 전압을 빼내고, 기준 전압과 비교해서 그 전류값에 따른 펄스폭으로 스위칭시켜 평균전류를 일정하게 유지하는 방식이다.
여기에는 전압비교부에서 모타내부의 권선전류의 상/하한선을 정하고 그 전류값에 따라서 스위칭시간을 정하는 방식 ( 이는 스테핑모타의 부하토르크와 속도 등에 따라 스위칭주파수가 변화되므로 가급적이면 부하변동이 적은 사무기기 등과 같은 용도에 적합하다 )과 20kHz정도의 기준주파수발진기를 부가하여 이의 주기내에서 스위칭주기를 제어하는 방식
( 일반적으로 PWM ( Pulse-Width-Modulation)방식으로 불리며 부하변동폭이 큰 조건에서도 안정적으로 동작한다. 단, 고속운전의 경우 대개 권선에 대한 인가전압이 높아져 높은 열을 발생시킴으로 이에대한 적절한 보완대책이 필요하다. 또한 자동전류저하기능을 부가하여 모타정지시 전류를 낮춰줌으로써 온도상승을 일부 낮출 수도 있다 )이 있다.
정전압드라이브(Constant-Voltage-drive) :
모타에 일정한 전압을 거는 방식. 효율이 나쁘므로 대개 외부저항을 이용한 L/R드라이브 방식으로 사용하므로, 일반적인 정전압 드라이브라고 하면 보통 L/R드라이브를 가리킨다.
이 정전압드라이브에는 L/R드라이브방식과 전압변환드라이브 방식이 있다
L/R드라이브(L/R-Drive) :
정전압원을 이용하며 대개 모타의 정격전압보다 높은 전압을 사용한다.
이경우 모타의 급격한 발열이 일어나므로 외부저항을 부가하여 모타권선에 흐르는 전류값을 낮춰줘야 한다. 이렇게하면 모타의 권선내에서 전류상승의 시간정수가 커져 짧은 시간내에 전류상승이 원하는 값까지 도달하므로 고속운전이 가능해진다. 외부저항값을 크게하고 전원전압을 높게하면 고속에서의 토르크는 커지지만 저항에서의 소비전력이 따라서 커지므로 전체적인 소비전력효율은 떨어진다.
2전압드라이브/전압변환드라이브(Bi-Level-drive) :
모타의 정격전압보다 높은 것과 낮은 것의 2종류를 이용하는 방식과 모타의 정격전압과 같은 외부전원에 부가저항을 사용하여 모타내부에 인가되는 전압을 차별화하는 방식이 있다.
이는 정지시나 저속시에 저전압을 인가하고 일정한 속도에 이르면 고전압으로 바꿔 입력함으로써 정전류구동에 가까운 운전특성을 얻을 수 있다. 이는 보통 사무기기 등과 같이 대량생산용으로 많이 쓰인다. 때로는 과전압드라브라고도 한다.
정전류드라이브(Constant-Current-Drive) :
모타에 입력되는 전류를 항상 일정하게 하는 방식. 여기에 상기의 쵸핑드라이브방식의 회로를 채택하면 보다 우수한 고속특성과 효율을 얻을 수 있다.
마이크로스텝드라이브(Microstepping or Microstep-drive) :
권선에 인가되는 평균전류값을 세밀하게 가감시켜 넣어줘 고정자와 회전자간의 인력-반발력을 상간에 차이를 만들어 줌으로써 회전자가 일반구동시의 기본각도보다 작은 각으로 분할되어 회전한다. 이경우 모타의 소음과 진동이 적어 부드러운 운전이 가능해지는 장점이 있지만 정밀도는 좋아지지 않는다. 특히 정지위치와 운전프로램시 주의를 요한다.
2상여자방식(Full-step or 2-Phases-On) :
항시 4상중 2개상이 함께 입력전원을 받아들인 구동방식으로 일반적으로 많이 사용되는 방식이다. 출력토르크가 좋다.
1-2상여자방식(Half-step or 1-2-Phases-On) :
1상-2상-1상-2상 과 같이 교대적으로 펄스를 부여하는 방식이다.
이때의 스텝당 회전각도는 기본각의 1/2이며, 따라서 모타의 진동이 줄어들고 보다 고속운전이 가능하나 부하가 큰 경우 정지위치의 정밀도에 주의를 요한다.
4상여자방식(4-Phases-On) :
이는 8선모타를 사용하며 항시 4상에 펄스를 넣어 구동시키는 방식으로서 스텝당 회전각도는 기본각이며 2상스테핑모타에 비해 토르크변동도 적고 보다 고속주파수까지 사용이 가능하다.
이와 같이 보다 안정된 회전특성을 얻을 수 있으나 구동회로가 복잡해지고 코스트가 높아 그다지 많이 사용되지는 않는다.
3-4상여자방식(3-4-Phases-On) :
3-4상으로 펄스입력을 교대로 하는 방식이며 보다높은 분해능을 얻을 수 있고 진동도 적으므로 고정밀도를 요하는 기기에 사용된다. 1스텝각은 기본각의 1/2이다.
3.6 결선방식에 따른 모타정격특성의 변화비율
정격항목
유니폴라결선
(Unipolar)바이폴라직렬결선
(Bipolar-Series)바이폴라병렬결선
(Bipolar-Parallel)전압(Volts)
1
1.4
0.7
전류(Amps)
1
0.7
1.4
저항(ohms)
1
2.0
0.5
인덕턴스(mH)
1
4.0
1.0
최대정지 토르크
1
1.4
1.4
- ( 상기의 데이터는 당사의 유니폴라모타를 기준으로 하였을 때, 바이폴라직렬연결은 각 Com선을 off시킨채 각 4상만을 사용하는 것이며, 바이폴라병렬결선은 Bifilar 권선후(서구에서는 8선으로 리드선을 인출시킴) 내부에서 별도로 입력선끼리, 그리 출력선끼리 결선하여 최종적으로 4선을 인출시키는 바이폴라 형태임.
단, 상기의 바이폴라는 Monofilar권선한 바이폴라모타가 아님 - 이 모타는 별도의 모타정격 및 특성을 갖는다. )
3.7 기타
Axial Play ( or End-play ) :
모타샤프트에 외부의 힘이 작용시 축방향으로 움직이는 거리
Radial Play ( or Side-play ) :
모타샤프트에 직각방향으로 외부의 힘이 작용시 베어링자체의 공차, 베어링내측과 샤프트간의 공차, 베어링외측과 모타 케이스(Bracket)내측간의 공차등으로 인해 모타샤프트가 축의 외경동심원으로부터 움직이는 거리
정격허용하중(Overhung) :
모타축에 수직방향으로 부하를 걸 경우의 허용하중의 크기.
이 정격하중을 넘는 부하의 경우 모타의 특성에 변화가 생기거나 모타가 고장날수도 있다.
표준모델의 경우 모타샤프트에 모타취부면으로부터 약 5mm정도 떨어진 위치라면 최대부하를 걸 수 있으며, 모타 취부면으로부터 먼 위치에 부하를 걸 경우 허용부하의 크기는 급격히 작아진다. ( 5mm위치에서 최대허용하중을 100으로하면, 약 10mm의 위치에서는 60정도가 되며, 15mm위치에서는 45정도로 된다 )
시리즈별 부하 허용하중 또는 압력
시리즈명
샤프트 회전방향 허용하중 또는 압력(Kgf)
(모터 브라켙으로부터의 샤프트 거리 / mm)5
10
15
20
39Q
5
3.5
2.5
2
42Q
5
3.5
2.5
2
56R
12
8
6
5
56Q
12
8
6
5
EMS24-A
3
2
1.5
1
EMS26-B
4
3
2
1.5
EMS24-C
4
3
2
1.5
EMS28-H
35
30
25
20
EMS36-F
12
8
6
5
EMS36-H
35
30
25
20
- 정격허용하중(Thrust) :
모타축과 동일방향으로 부하를 걸 경우의 허용하중의 크기.
이 정격하중을 넘은 부하의 경우 모타의 특성에 변화가 생기거나 모타가 고장날 수도 있다.가급적이면 모타를 수평으로 세워 부하를 연결하는 것이 모타특성의 보호나 고장방지에 훨씬 효과적이다.- 자기동토르크(Pull-in Torque ) :
-

- 1. FARADAY’S 법칙 :
- 1830년경 Michael
Faraday와 Joseph Henly가 거의 동시에 변화하는 자기장과 감긴
도선내에 유도되는 유도기전력(EMF)사이에 어떠한 상관관계가 있는지를
밝혀내었다. 결과는 어떠한 자기장(B:자속밀도)속을 도선이
어떠한 속도(V)로 움직일 때 이 도선에 유도되는 유도기전력(E)는
Vector함수로서 아래와 같은 관계식을 갖는다.
E = B x V
이 도선의 저항을 r이라고 하면, 이 도선에 유기되는 전류(I)는
I = E/r = B x V/r
이 된다.
이 관계를 전기모타에 응용한 것이 플레밍의 왼손법칙과 오른손법칙으로 전개된 것이다.
즉, 길이 L의 도선에 전류 I를 흘렸을 때, 자기장으로부터 받는 이 도선의 자기력F는
F = BLIsinθ( θ: 도선이 자기장의 방향과 이루는 각도 )
가 된다.
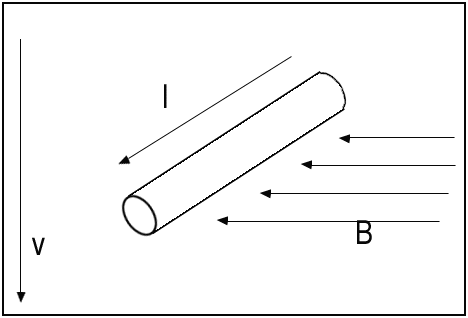
즉, F는 항상 B와 I의 직각방향으로 발생한다는 점이 중요하다.
이와 같이 Faraday’s법칙과 플레밍의 법칙은 때로는 같은 원리로 간주되기도하며, 경우에 따라서는 혼용하여 사용하기도 한다.
1-1. 플레밍의 왼손법칙 :
모터의 내부에서 로타(회전자)에 작용하는 힘의 원리를 설명하는 것이다.
이는 일정한 크기의 자계속에 하나의 도선을 놓아두고, 이 도선에 전류를 흘리면 도선에 힘이 작용하게된다. 이때, 전류와 힘, 그리고 자계의 방향사이의 관계를 나타낸 것이 왼손법칙이다. ( 단, 이것은 회전자에 도선을 감았을 경우 바로 적용이 되나, 회전자가 자석으로 되어있고, 고정자에 도선을 감아 여기에 전류를 흘려줄 경우는 도선이 받는 힘의 방향과 반대방향으로 회전자가 힘을 받게된다. )
이 왼손법칙은 F = B x V = B x Ir 의 벡터의 곱으로 표시된다.
1-2. 플레밍의 오른손법칙 :
이것은 일정한 자계속에 놓여있는 도선을 외부의 힘으로 움직여주었을 때 움직이는 도선에 유도전류가 흐르게 된다. 이때 움직이는 속도와 자계의 방향, 그리고 전류의 방향사이의 관계를 나타낸 것이 오른손 법칙으로서, 이를 발전기의 원리라고도 한다.
E = F x B or -E = B x F 의 벡터의 곱으로 표시된다.
즉, 도선에 생기는 유도전압은 회전자의 속도에 비례하여 커진다.
1-3. 모터내부에서의 플레밍의 왼손법칙과 오른손법칙과의 관계 :
외부에서 고정자(Stator)에 감긴 도선에 전류를 흐르게하면, 회전자(Rotor)의 자계와 작용하여 회전자가 움직이게 된다. 그러나, 일단 회전자가 움직이게 되면, 이는 고정된 자계속을 도선이 움직이는 것과 같은 효과가 발행되므로 동일 도선에 회전속도에 비례하여 반대방향의 역기전압이 발생된다. 따라서 외부에서 흘려주는 입력전류와 반대방향의 역기전압(전류)는 서로 상쇄되어 실제로 도선속을 흐르는 전류를 제한하게 되고, 이로써 모타의 회전속도와 이 속도에서의 토르크를 제한하게 된다.
즉, 최대속도에서는 토르크가 0 이 된다.- 3. Faraday의 법칙과
플레밍의 법칙은 DC모타의 기본응용원리이다
- 아래의 그림과 같이 어떠한 자기장속에 권선된 도선의 양끝에 외부전류가 연결되어 있다고 하면
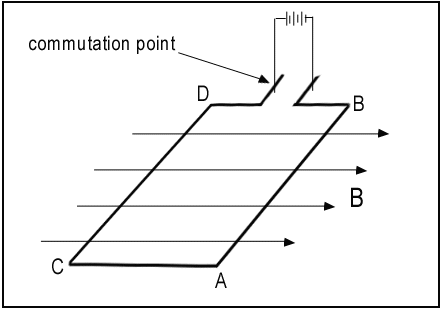
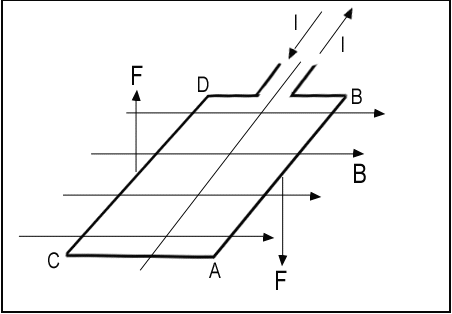
이 그림에서 보는 바와같이 도선AB부분은 아래방향으로 향하는 자기력을 받게되고 도선 CD는 윗방향으로 향하는 자기력을 받게된다 ( 단, 도선 AB와 CD에 작용하는 자기력은 힘의 크기는 같으나 방향만 다를뿐이다 ). 이 힘은 외부전류가 도선의 양끝에 연결되어 있을때는 자기력의 영향을 받으나, 점차 회전함에 따라 외부전류와 연결되지 못하므로 자기력은 사라지고 남는 것은 관성운동에너지( Rotational Kinetic Energy ) 만으로 회전운동을 계속하게 되는 것이다.
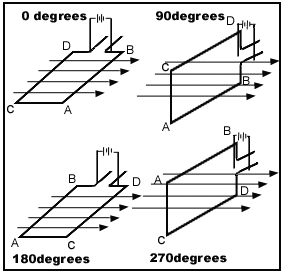
이 도선이 다시 정 반대방향인 180˚의 위치에 오게되면 외부전류와 다시 연결되어 전류가 BACD로 흐르게되어, 도선 BA는 윗방향으로 CD는 아랫방향으로 다시 자기력의 영향을 받아 다시 회전력을 얻게된다.
- 아래의 그림과 같이 어떠한 자기장속에 권선된 도선의 양끝에 외부전류가 연결되어 있다고 하면
- 이와
같이 도선은 회전을 계속하게된다.
이렇게 해서 얻어진 도선이 받는 토르크의 변화를 그려보면 아래의 그림과 같다.
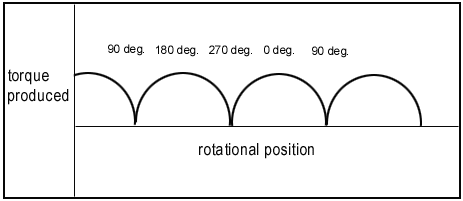
이와 같이 외부전류에 연결된 모타라면 토르크변화( Torque-ripple )가 너무커서 결국 부하를 연결했을 경우 모타의 진동 때문에 거의 쓸 수가 없을 것이다.만일 외부전류가 90˚/270˚에 추가로 연결될 수 있다면 발생되는 토르크의 변화는 아래와 같아질 것이다.
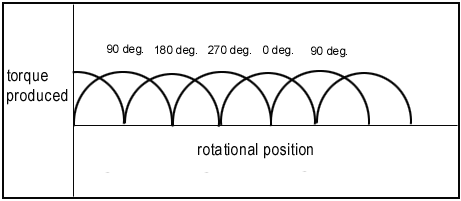
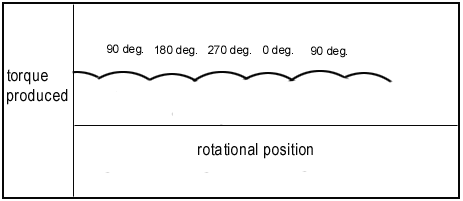
이러한 원리를 응용하여 실용적인 모타로 만들자면, 우선은 토르크의 향상을 위하여도선의 수를 증가시켜야하고, 또한 모타의 진동 ( 토르크-리플 )을 줄이기 위하여 외부전류와의 접속 ( 정류자 : Commutator 와 브러시 : Brush )수를 충분히 늘려주어야 한다.
모타의 토르크 는 어떻게 결정되는 것인가를 생각해보자.
만일 도선이 1선만으로 이루어져 있다면,
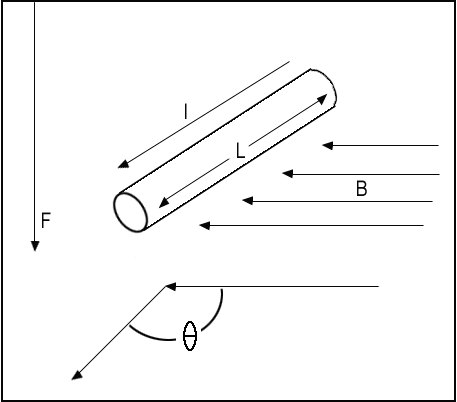
우선 이 도선이 자기장에 직각방향으로 있다고 하면 도선 AB가 받는 힘은
F = BLIsinθ ( θ: 도선이 자기장과 이루는 각도 ) = BLI
가 될 것이다. 이제 이 모타가 도선이 1선만이 아닌 N개의 도선으로 감아져 있다고하면 도선 AB군이 받는 힘은
F = NBLI
가 될 것이다.
도선이 감겨진 축중심으로부터 도선 AB까지의 거리를 R이라고 하면, 이 축중심에 생기는 토르크의 크기는
T = FR = RNBLI
가될 것이고, 반대편의 도선 CD 역시 도선 AB와 같은 크기의 토르크를 얻게 될 것이므로 결과적으로 발생되는 출력토르크는
T = 2FR = 2RNBLI
가 될 것이다.
-
- 4. DC모타의 특성관련 해설 :
- 4. DC모타의 특성관련 해설 :
- 4.1
Kirchoff’s 원리 :
어떤 폐회로( a Circuit loop )내에서의 전위차 증가분의 합은 전위차감소의 합과 같다.
4.2 Kirchoff’s원리의 응용 :
DC모타에 직렬로 외부에서 DC전원을 연결하여주면, 이 외부전압은 모타의 권선된 도선에 걸리는 전압과 회전자에 의해 발생된 역기전압의 합과 같다는 것이다.
즉, V□ = ( I x R ) + Ve
V□ = 외부전원에서 공급된 전압
I = 모타의 도선에 흐르는 전류
R = 모타 도선의 저항값
Ve= 역기전압 ( 유도기전력 ) : 이는 회전자의 각속도에 직접비례한다.
모타자체의 각속도에 의한 역기전력발생과 관련된 비례상수를 Ke ( 역기전압계수 )라고 하면,
Ve= S x Ke ( S : 모타의 각속도 )
따라서, V □= ( I x R ) + Ve= ( I x R ) + ( S x Ke )
≫ Ke : 보통 DC모타 설계시 Volt/RPM 또는 mV/RPM 의 값을 표시해준다.
이는 도선의 권선조건과 고정자와 회전자간의 공극(Airgap)내에서 자기력선의 방향 등과 밀접한 관계가 있다. 보통 제조자는 다음의 관련상수값을 제공한다.( 역기전력상수, 토르크상수, 속도상수 )
토르크상수는 권선된 도선내에 흐르는 전류에 비례하는 상수이므로
T = I x Kt ( T : 회전자에 발생되는 토르크, Kt : 토르크상수 )
따라서, V = ( T x R ) / Kt + ( S x Ke )
이때 모타자체의 마찰부하토르크를 Tf, 외부의 기계적부하에 의한 토르크를 Tl 이라고 하면, T = Tf + Tl
또 외부전원이 안정되고 일정한 전압이라면, 모타의 속도는 마찰부하토르크와 외부의 부하토르크의 합에 비례하게 될 것이다. 이 비례상수가 곧 “ 토르크-속도 곡선 ( Speed-Torque-Curve) “ 이다.
상기의 관계식을 바꾸어보면 모타의 속도 S 는
S = Vo / Ke ? Tl / ( Kt x Ke )
이것을 외부부하토르크의 변화에 대한 속도S를 보게되면,
dS / dTl = -R / ( Kt x Ke )
와 같이 외부부하토르크가 증가할수록 속도는 비례하여 감소된다.
이제 어느부하를 모타에 인가하여 모타를 구동시킬 경우 이때의 모타사용효율을 구해보면, 모타의 무부하전류를 Ao, 부하토르크를 Tl, 무부하속도를 So, 그리고 토르크-속도커브의 비례상수를 Ko라고 할 때,부하토르크에 의한 속도감소분 Sb = -Tl x ( So / Ko )가 되고,실제로 부하를 가진 모타의 속도는 S = So -Sb가 된다.
모타 내부에 흐르는 전류에 따라 변화하는 부하토르크상수 Kt 값으로부터,부하로 인해 증가된 전류값을 구해보면 Al = Tl x Kt,
따라서 모타의 도선내에 흐르는 총 전류값 I = Ao + Al
이 때의 모타의 기계적인 출력P는 Pout = S x Tl x 0.1047 ( watt )
( 0.1047값은 부하토르크의 단위가 N-m이고, 속도단위가 RPM일 때 소비전력(Watt)으로의 단위변환계수값임 : “ 5. 모타의 단위계해설 “ 참조 )
모타의 기계적입력은 외부전압과 모타의 총 전류값을 곱한 값이므로,
Pin = I x Vin ( watt )
따라서 이때의 모타사용효율 E = Pout / Pin x 100 ( % ) 가 된다. -
- 5. 모타의 단위계 해설 :
5.1 소비전력 ( Power = 일률 ) :
물리적으로 Power(일률)라고 하면 단위시간당 주어진 힘과 작용한 거리의 곱을 의미한다. DC모타와 같은 회전운동의 경우라면, 이 Power(일률)는 단위시간당 단위시간당 주어진 토르크와 작용한 회전거리의 곱과 같다.
P = T x Z
( P = 기계적인 회전운동일율, T = 토르크 )
( Z = D / t : Z=회전속도, D=회전거리, t=시간 )
일반적으로 회전속도Z의 단위로서 RPM ( Revolutions per Minute :분당 회전수 )로 타나내며, 소비전력을 구하기 위해서는 이 속도를 “ rad / sec “ 로 바꿔줘야 한다.
1 rad = 360˚/2 π
( rad = 반지름과 회전원주의 길이의 비로 각을 표시하는 단위로서 반지름과 회전원주의 길이가 같아지는 각도를 1rad라한다. )
따라서 각속도 Z (rad/sec) = RPM x 2π/60sec 가 된다.
이렇게 토르크-속도 관계를 Power(Watt)로 변환계산에 아주 유용한 단위변환관계수치를 적어보면 아래와 같다.
단위변환관계수치토르크 단위
속도단위
변환계수
oz-in
RPM
0.00074
oz-in
rad/sec
0.0071
in-lb
RPM
0.0118
in-lb
rad/sec
0.1130
ft-lb
RPM
0.1420
ft-lb
rad/sec
1.3558
N-m
RPM
0.1047
N-m
rad/sec
1.0002
(예1) 부하토르크 3 oz-in를 500RPM으로 운전하는 데 필요한 소비전력을 계산해보자.
P = T x Z의 식에서
P = 3(oz-in) x 500(RPM) x 0.00074 = 1.11(Watt)
(예2) 중심축으로부터의 거리 a(m)에 질량 M(kg), 이 물체의 회전반경을 k(m)인 풀리에 줄을 감아 이 줄에 F(N)의 힘을 가했을 때, 이 풀리의 각가속도는 ?
( 단, 마찰부하토르크는 b라고 하자. )
이 물체의 관성모멘트는
I = M(k.k) (kgm.m) 이며,
이 때의 각가속도는
α = {[ Fa(Nm) - b(Nm)] / I(kgm.m)} ( rad/sec.sec)를 얻게된다.
5.2 참고를 위한 단위계 :
N ( Newton ) : 힘의 단위로서 1kg의 질량에 1m/sec.sec의 가속도를 일으키는 힘
1 N = 1kgm/sec.sec = 10^-5dyne ( 1 dyne = 1gcm/secsec )
lb ( Pound ) : 영국계의 힘의 단위로서 1 lb = 4.45N 정도가 된다.
Nm : 토르크의 단위
J ( Joule ) : 일의 단위로서 1J = 1Nm
W ( Watt) : 일률의 단위로서 1W = 1 J/sec 이다.
Hp (Horse-Power) : 역시 일률의 단위로서 1hp = 750W 이다.
5.3 토르크의 단위 환산표
Nm
mNm
Ncm
kgcm
oz-in
lb-in
1
1000
100
10.197
141.62
8.851
0.01
10
1
0.102
1.4162
0.0885
0.098
98
9.8
1
13.877
0.8679
0.007
7.062
0.706
0.072
1
0.0625
0.113
113
11.3
1.152
16
1
5.4 관성모멘트의 단위환산표
kgcm²
kgcm.sec²
oz-in²
oz-in.sec²
lb-in²
lb-in.sec²
1
1.02x10-³
5.467
1.42x10-²
0.342
8.85x10-⁴
0.183
1.87x10-⁴
1
2.59x1-³
6.25x10-²
1.62x10-⁴
2.926
2.98x10-³
16
4.14x10-²
1
2.59x10-³
-
- 6. 스테핑모타의 구동원리 :
- 아래그림과 같이
회전자(Rotor)둘레에 50개의 치(Teeth)가 있고, 고정자(Stator)의
내경에 48개의 치가 있는 모타를 예로 들어보자.
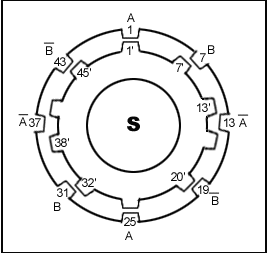
- 그림에서 보는 바와같이 고정자의 치피치(Tooth-pitch)는 7.5˚이고 회전자의 치피치는 7.2˚이다. 따라서 회전자의 치 r 과 고정자의 치 s는 최소 0.3˚의 각도차를 가지고 있게된다.이제 A상을 여자시키면 회전자의 r1번과 고정자의 s1번, 그리고 r26번과 s25번치가 일치(Alignment)하게 된다. 이제 A상을 off하고 B상을 여자시키면 r7번과 s7번치, 그리고 r32번과 s31번치가 일치하도록 회전을 하게된다 ( 이는 고정자의 실질 상수가 8개이므로 A상을 여자시켰을 때 일치한 회전자의 치로부터 다음 B상에 가장 가까운 회전자의 치는 A상을 여자시켰을 때 일치한 치로부터 7 번째치가 되기 때문이다. ). A상을 여자시켰을 때 r7과 s7의 각도차는
( 7.5˚ - 7.2˚ ) x 6 = 1.8˚
이기 때문에 기본회전스텝각은 1.8˚가 된다.
회전방향을 반대로 하고자하면 상기의 여자순서를 반대로 하면 된다.
실질적인 고정자와 회전자의 구조는 아래와 같다.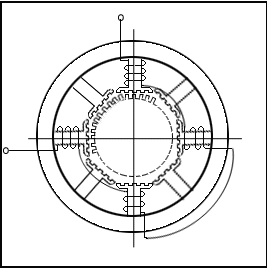
- 그림에서 보는 바와같이 고정자의 치피치(Tooth-pitch)는 7.5˚이고 회전자의 치피치는 7.2˚이다. 따라서 회전자의 치 r 과 고정자의 치 s는 최소 0.3˚의 각도차를 가지고 있게된다.이제 A상을 여자시키면 회전자의 r1번과 고정자의 s1번, 그리고 r26번과 s25번치가 일치(Alignment)하게 된다. 이제 A상을 off하고 B상을 여자시키면 r7번과 s7번치, 그리고 r32번과 s31번치가 일치하도록 회전을 하게된다 ( 이는 고정자의 실질 상수가 8개이므로 A상을 여자시켰을 때 일치한 회전자의 치로부터 다음 B상에 가장 가까운 회전자의 치는 A상을 여자시켰을 때 일치한 치로부터 7 번째치가 되기 때문이다. ). A상을 여자시켰을 때 r7과 s7의 각도차는
-

- 본 추천사이트는 각종 모타와 관련된 기술적인 내용을 기술한 홈페이지들을 소개하는 곳입니다.
1. 스테핑모타 관련 사이트 - 1.1
일반교육용 프로그램 사이트 :
- www.cs.uiowa.edu/~jones/step : 스테핑모타의 기초 이해
- http://consys.yeungnam.ac.kr/~sglee/info/step/step_motor.html
- http://home.mira.net/~tonymerc/steptheo/steptheo.htm : stepping motor 의 기초이론
- http://www.eio.com/jasstep.htm#types : working with stepper motor
1.2 전문가용 기술관련 사이트
- www.cs.uiowa.edu/~jones/step/circuits.html : 제어회로의 기초이론
- www.cs.uiowa.edu/~jones/step/current.html : 고속운전 제어회로의 전압/전류제어이론 및 PWM제어이론
- www.cs.uiowa.edu/~jones/step/micro.html : 마이크로스테핑 제어이론
- www.cs.uiowa.edu/~jones/step/midlevel.html : 응용제어 (중급)
- www.cs.uiowa.edu/~jones/step/highlevel.html : 응용제어 (고급)
- www.cs.uiowa.edu/~jones/step/example.html : 제어회로의 예
- http://members.tripod.com/~schematics/stepper2.htm : stepping motor controller 회로도
- http://www.euclidres.com/apps/stepper_motor/stepper.html : stepping motor의 구동방식에 따른 accuracy의 고찰
- http://www.cadvision.com/blanchas/hexfet : MOSFET의 switching application에 대하여
- http://www.eio.com/crntctrl.htm : current control in stepping motor
- 1.3 사용상 기술문제에 대한 토론 사이트
2. 일반 DC모타 관련 사이트- 2.1
일반교육용 사이트 :
- www.micromo.com/03application_notes/tutorial1.asp : 전자기학과 DC모타
- http://www.engin.umich.edu/group/ctm/examples/motor/digital.html
"미국 Michigan 대학의 사이버 강의자료"로서 Digital DC Motor with PID Control 에 관한 자료
- http://www.educatorscorner.com/experiments/html/exp78.html : "미국 Illinois 대학교 Dan Block 교수의 자료로서 Introduction to the DC Motor
-http://www.eece.ksu.edu/~starret/589/man/589toc.html : DC Motor 관련 전반적으로 해설
-http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/motdc.html : DC모타의 동작원리를 동영상으로 보여주는 교육사이트.
2.2 전문가용 기술관련 사이트
- http://www.pmdi.com/php2.php : Torque-Speed Calculator Applet(JAVA언어로 되어있음)
- http://cadvision.com/blanchas/hexfet/ : "호주 Swinburne University of Technology" 의 사이버 강의자료로서 DC Motor Control을 위한 MOSFET에 관한 교육자료
2.3 사용상 기술문제에 대한 토론 사이트
3. BLDC모타 관련 사이트- 3.1
일반교육용 사이트
-http://rose-hulman.edu/~nordjp/ :3상 Brushless DC Motor 관련 용어해설 및 기초지식 소개
3.2 전문가용 기술관련 사이트
3.3 사용상 기술문제에 대한 토론 사이트 일
4. AC모타 관련 사이트- 4.1
일반교육용 사이트
-http://www.instantweb.com/o/oddparts/acsi/motortut.htm : AC 모타에 대한 사이버 관련자료.
4.2 전문가용 기술관련 사이트
4.3 사용상 기술문제에 대한 토론 사이트 일
5. 서보모타 관련 사이트- - http://www.hvwtech.com/about_servos.htm : servo 모타에 대한 기초
- http://www.pittmannet.com/220000.html : DC Servo Motor 의 부하토크, 속도, 열관계 등에 대한 계산방식의 소개
6. 기타 모타관련 사이트
- http://www.ericsson.se/microe/apn_ind.html : stepping motor용 IC
- http://eu.st.com/stonline/bin/fts.exe : stepping motor 용 IC
- http://members.tripod.com/~schematics/symbols.htm : common circuit symbols
- http://members.tripod.com/~schematics/ohmslaw.htm : Ohm's law chart
- http://members.tripod.com/~schematics/resistor.htm : Reading resistor'value- - http://www.iserv.net/~alexx/lib/motors.htm : 각종 모타 및 관련기술 사이트 종합 모음 자료
- - http://www.hvwtech.com/about_servos.htm : servo 모타에 대한 기초